Definition 10.3.1. Reflexive Relation.
Let \(A\) be a set and let \(R\) be a relation on \(A\text{.}\) Then \(R\) is reflexive if and only if \(a R a\) for all \(a \in A\text{.}\)
Section 10.3 Properties of Relations
Subsection 10.3.1 Individual Properties
Consider the set \(B = \{1, 2, 3, 4, 6, 12, 36, 48\}\) and the relations “divides” and \(\leq \) on \(B\text{.}\) We notice that these two relations on \(B\) have three properties in common:
- Every element in \(B\) divides itself and is less than or equal to itself. This is called the reflexive property.
- If we search for two elements from \(B\) where the first divides the second and the second divides the first, then we are forced to choose the two numbers to be the same. In other words, no two different numbers are related in both directions. The reader can verify that a similar fact is true for the relation \(\leq \) on \(B\text{.}\) This is called the antisymmetric property.
- Next if we choose three values (not necessarily distinct) from \(B\) such that the first divides the second and the second divides the third, then we always find that the first number divides the third. Again, the same is true if we replace “divides” with “is less than or equal to.” This is called the transitive property.
Relations that satisfy these properties are of special interest to us. Formal definitions of the properties follow.
Definition 10.3.2. Antisymmetric Relation.
Let \(A\) be a set and let \(R\) be a relation on \(A\text{.}\) Then \(R\) is antisymmetric if and only if whenever \(a R b\) and \(a \neq b\) then \(b R a\) is false.
An equivalent condition for antisymmetry is that if \(a R b\) and \(b R a\) then \(a = b\text{.}\) You are encouraged to convince yourself that this is true. This condition is often more convenient to prove than the definition, even though the definition is probably easier to understand.
A word of warning about antisymmetry: Students frequently find it difficult to understand this definition. Keep in mind that this term is defined through an “If...then...” statement. The question that you must ask is: Is it true that whenever there are elements \(a\) and \(b\) from \(A\) where \(a R b\) and \(a \neq b\text{,}\) it follows that \(b\) is not related to \(a\text{?}\) If so, then the relation is antisymmetric.
Another way to determine whether a relation is antisymmetric is to examine (or imagine) its digraph. The relation is not antisymmetric if there exists a pair of vertices that are connected by edges in both directions.
Definition 10.3.3. Transitive Relation.
Let \(A\) be a set and let \(R\) be a relation on \(A\text{.}\) \(R\) is transitive if and only if whenever \(a R b\) and \(b R c\) then \(a R c\text{.}\)
Subsection 10.3.2 Partial Orderings
Not all relations have all three of the properties discussed above, but those that do are a special type of relation.
Definition 10.3.4. Partial Ordering.
A relation on a set \(A\) that is reflexive, antisymmetric, and transitive is called a partial ordering on \(A\text{.}\) A set on which there is a partial ordering relation defined is called a partially ordered set or poset.
Example 10.3.5. Set Containment as a Partial Ordering.
Let \(A\) be a set. Then \(\mathcal{P}(A)\) together with the relation \(\subseteq\) (set containment) is a poset. To prove this we observe that the three properties hold, as discussed in Chapter 4.
- Let \(B \in \mathcal{P}(A)\text{.}\) The fact that \(B \subseteq B\) follows from the definition of subset. Hence, set containment is reflexive.
- Let \(B_1, B_2 \in \mathcal{P}(A)\) and assume that \(B_1\subseteq B_2\) and \(B_1\neq B_2\) . Could it be that \(B_2\subseteq B_1\text{?}\) No. There must be some element \(a\in A\) such that \(a \notin B_1\text{,}\) but \(a\in B_2\text{.}\) This is exactly what we need to conclude that \(B_2\) is not contained in \(B_1\text{.}\) Hence, set containment is antisymmetric.
- Let \(B_1, B_2,B_3 \in \mathcal{P}(A)\) and assume that \(B_1 \subseteq B_2\) and \(B_2 \subseteq B_3\) . Does it follow that \(B_1 \subseteq B_3\) ? Yes, if \(a\in B_1\text{,}\) then \(a\in B_2\) because \(B_1 \subseteq B_2\text{.}\) Now that we have \(a\in B_2\) and we have assumed \(B_2 \subseteq B_3\text{,}\) we conclude that \(a\in B_3\text{.}\) Therefore, \(B_1\subseteq B_3\) and so set containment is transitive.
Figure 10.2.6 is the graph for the “set containment” relation on the power set of \(\{1,2\}\text{.}\)
Figure 10.2.6 is helpful insofar as it reminds us that each set is a subset of itself and shows us at a glance the relationship between the various subsets in \(\mathcal{P} (\{1,2\})\text{.}\) However, when a relation is a partial ordering, we can streamline a graph like this one. The streamlined form of a graph is called a Hasse diagram or ordering diagram. A Hasse diagram takes into account the following facts.
- By the reflexive property, each vertex must be related to itself, so the arrows from a vertex to itself (called “self-loops”) are not drawn in a Hasse diagram. They are simply assumed.
- By the antisymmetry property, connections between two distinct elements in a directed graph can only go one way, if at all. When there is a connection, we agree to always place the second element above the first (as we do above with the connection from \(\{1\}\) to \(\{1,2\}\)). For this reason, we can just draw a connection without an arrow, just a line.
- By the transitive property, if there are edges connecting one element up to a second element and the second element up to a third element, then there will be a direct connection from the first to the third. We see this in Figure 10.2.6 with \(\emptyset\) connected to \(\{1\}\)\(\)and then \(\{1\}\) connected to \(\{1,2\}\text{.}\) Notice the edge connecting \(\emptyset\) to \(\{1,2\}\text{.}\) Whenever we identify this situation, remove the connection from the first to the third in a Hasse diagram and simply observe that an upward path of any length implies that the lower element is related to the upper one.
Using these observations as a guide, we can draw a Hasse diagram for \(\subseteq\) on \(\{1,2\}\) as in Figure 10.3.6.
Example 10.3.7. Definition of a relation using a Hasse diagram.
Consider the partial ordering relation \(R\) whose Hasse diagram is Figure 10.3.8.
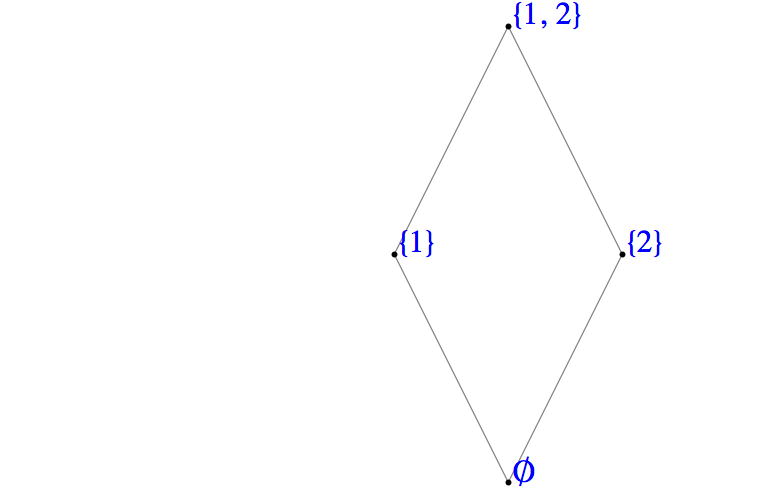
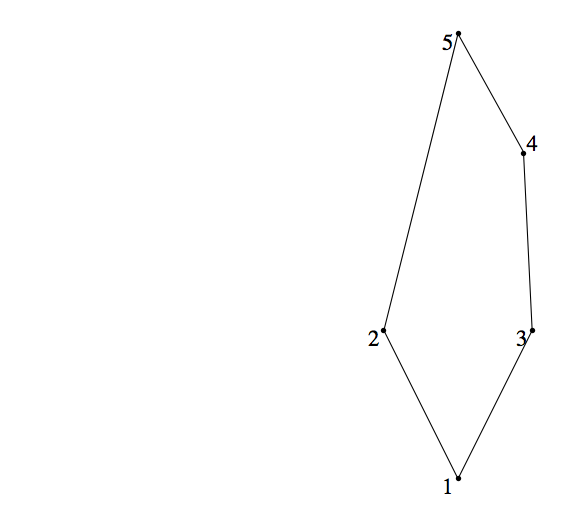
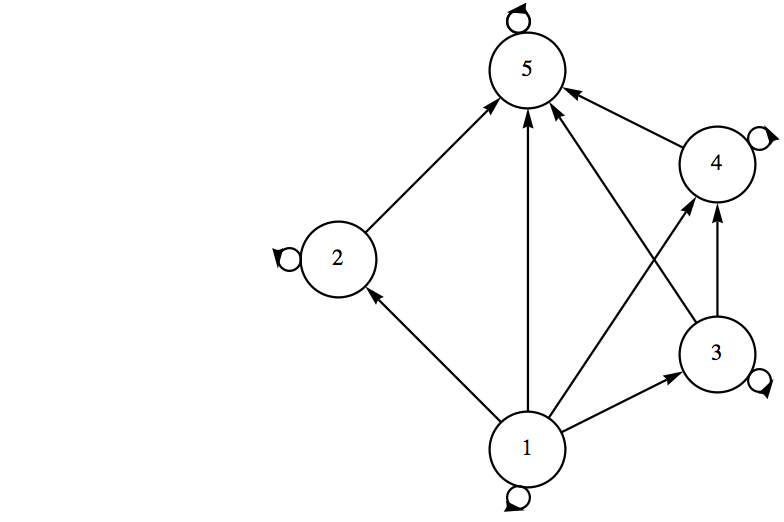
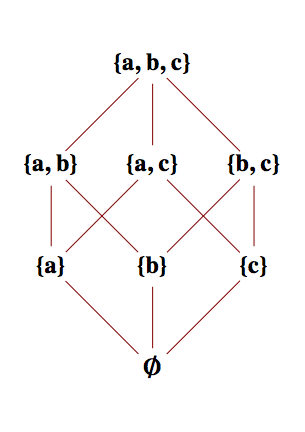
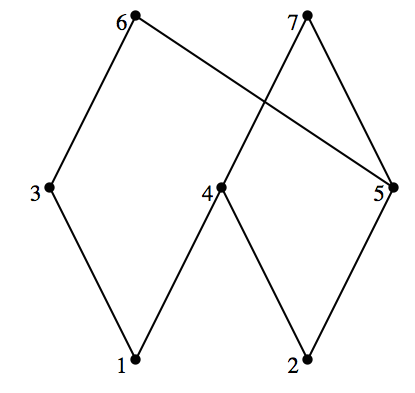
How do we read this diagram? What is \(A\text{?}\) What is \(R\text{?}\) What does the digraph of \(R\) look like? Certainly \(A = \{1,2,3,4,5\}\) and \(1 R 2\text{,}\) \(3 R 4\text{,}\) \(1 R 4\text{,}\) \(1 R 5\text{,}\) etc., Notice that \(1 R 5\) is implied by the fact that there is a path of length three upward from 1 to 5. This follows from the edges that are shown and the transitive property that is presumed in a poset. Since \(1 R 3\) and \(3 R
4\text{,}\) we know that \(1 R 4\text{.}\) We then combine \(1 R 4\) with \(4 R 5\) to infer \(1 R 5\text{.}\) Without going into details why, here is a complete list of pairs defined by \(R\text{.}\)
\begin{equation*}
R = \{(1,1),(2,2),(3,3),(4,4),(5,5),(1,3),\\
(1,4),(1,5),(1,2),(3,4),(3,5),(4,5),(2,5)\}
\end{equation*}
A digraph for \(R\) is Figure 10.3.9. It is certainly more complicated to read and difficult to draw than the Hasse diagram.
A classic example of a partial ordering relation is \(\leq \) on the real numbers, \(\mathbb{R}\text{.}\) Indeed, when graphing partial ordering relations, it is natural to “plot” the elements from the given poset starting with the “least” element to the “greatest” and to use terms like “least,” “greatest,” etc. Because of this the reader should be forewarned that some texts use the symbol \(\leq\) for arbitrary partial orderings. This can be quite confusing for the novice, so we continue to use generic letters \(R\text{,}\) \(R\text{,}\) etc.
Subsection 10.3.3 Equivalence Relations
Another common property of relations is symmetry.
Definition 10.3.10. Symmetric Relation.
Let \(R\) be a relation on a set \(A\text{.}\) \(R\) is symmetric if and only if whenever \(a R b\text{,}\) it follows that \(b R a\text{.}\)
Consider the relation of equality defined on any set \(A\text{.}\) Certainly \(a = b\) implies that \(b = a\) so equality is a symmetric relation on \(A\text{.}\)
Surprisingly, equality is also an antisymmetric relation on \(A\text{.}\) This is due to the fact that the condition that defines the antisymmetry property, \(a = b\) and \(a \neq b\text{,}\) is a contradiction. Remember, a conditional proposition is always true when the condition is false. So a relation can be both symmetric and antisymmetric on a set! Again recall that these terms are not negatives of one other. That said, there are very few important relations other than equality that are both symmetric and antisymmetric.
Definition 10.3.11. Equivalence Relation.
A relation \(R\) on a set \(A\) is called an equivalence relation if and only if it is reflexive, symmetric, and transitive.
The classic example of an equivalence relation is equality on a set \(A\text{.}\) In fact, the term equivalence relation is used because those relations which satisfy the definition behave quite like the equality relation. Here is another important equivalence relation.
Example 10.3.12. Equivalent Fractions.
Let \(\mathbb{Z}\)* be the set of nonzero integers. One of the most basic equivalence relations in mathematics is the relation \(Q\) on \(\mathbb{Z}\times \mathbb{Z}^*\) defined by \((a, b) Q(c, d)\) if and only if \(a d = b c\text{.}\) We will leave it to the reader to, verify that \(Q\) is indeed an equivalence relation. Be aware that since the elements of \(\mathbb{Z}\times \mathbb{Z}^*\) are ordered pairs, proving symmetry involves four numbers and transitivity involves six numbers. Two ordered pairs, \((a, b)\) and \((c, d)\text{,}\) are related if the fractions \(\frac{a}{b}\) and \(\frac{c}{d}\) are numerically equal.
Our next example involves the following fundamental relations on the set of integers.
Definition 10.3.13. Congruence Modulo \(m\).
Let \(m\) be a positive integer, \(m\geq 2\text{.}\) We define congruence modulo m to be the relation \(\equiv_m\) defined on the integers by
\begin{equation*}
a \equiv_m b \Leftrightarrow m \mid (a-b)
\end{equation*}
We observe the following about congruence modulo \(m\text{:}\)
- This relation is reflexive, for if \(a \in \mathbb{Z} \text{,}\) \(m \mid (a-a) \Rightarrow a\equiv_ma \text{.}\)
- This relation is symmetric. We can prove this through the following chain of implications.\begin{equation*} \begin{split} a \equiv_m b &\Rightarrow m \mid (a-b)\\ & \Rightarrow \textrm{For some } k \in \mathbb{Z}, a-b = m k \\ & \Rightarrow b-a = m (-k)\\ & \Rightarrow m \mid (b-a)\\ & \Rightarrow b \equiv_m a \end{split}\text{.} \end{equation*}
- Finally, this relation is transitive. We leave it to the reader to prove that if \(a \equiv _mb \) and \(b\equiv _mc\text{,}\) then \(a \equiv _mc\text{.}\)
Frequently, you will see the equivalent notation \(a \equiv b (\textrm{mod } m)\) for congruence modulo \(m\text{.}\)
Example 10.3.14. Random Relations usually have no properties.
Consider the relation s described by the digraph in Figure 10.3.15. This was created by randomly selecting whether or not two elements from \(\{a,b,c\}\) were related or not. Convince yourself that the following are true:
- This relation is not reflexive.
- It is not antisymmetric.
- Also, it is not symmetric.
- It is not transitive.
- Is \(R\) an equivalence relation or a partial ordering?
Not every random choice of a relation will be so totally negative, but as the underlying set increases, the likelihood any of the properties are true begins to vanish.
Exercises 10.3.4 Exercises
1.
- Let \(B = \{a, b\}\) and \(U = \mathcal{P}(B)\text{.}\) Draw a Hasse diagram for \(\subseteq \) on \(U\text{.}\)
- Let \(A = \{1,2, 3, 6\}\text{.}\) Show that divides, \(\mid \text{,}\) is a partial ordering on \(A\text{.}\)
- Draw a Hasse diagram for divides on \(A\text{.}\)
- Compare the graphs of parts a and c.
Answer.
- See Figure 10.3.16.
- \(\mid\) on \(A\) is reflexive because \(\forall a \in A, a \mid a\) is true and \((a,a) \in \) the relation. \(\mid\) on \(A\) is antisymmetric because \(\forall a, b \in A\) if \(a \mid b\) is true and \((a,b) \in \) the relation, then \(b \mid a\) is not true and \((b,a) \notin \) the relation, unless \(a = b\text{.}\) \(\mid\) on \(A\) is transitive because \(\forall a, b, c \in A\text{,}\) if \((a,b)\) and \((b,c) \in\) the relation, then \(a|b\) and \(b|c\text{.}\) Therefore \(ak =b\) for some integer \(k\) and \(bj = c\) for some integer \(j\text{.}\) Thus \(akj = c\text{,}\) \(a|c\text{,}\) and \((a,c) \in\) the relation. Therefore \(\mid\) on \(A\) is a partial ordering.
- See Figure 10.3.16.
- The graphs are the same if we disregard the names of the vertices.
2.
Repeat Exercise 1 with \(B = \{a, b, c\}\) and \(A = \{1, 2, 3, 5, 6, 10, 15, 30\}\text{.}\)
Hint.
Here is a Hasse diagram for the part (a).
3.
Consider the relations defined by the digraphs in Figure 10.3.18.
- Determine whether the given relations are reflexive, symmetric, antisymmetric, or transitive. Try to develop procedures for determining the validity of these properties from the graphs,
- Which of the graphs are of equivalence relations or of partial orderings?
Answer.
Table 10.3.19. Properties of relations defined by given digraphs Part reflexive? symmetric? antisymmetric? transitive? i yes no no yes ii yes no yes yes iii no no no no iv no yes yes yes v yes yes no yes vi yes no yes yes vii no no no no - Graphs ii and vi show partial ordering relations. Graph v is of an equivalence relation.
4.
Determine which of the following are equivalence relations and/or partial ordering relations for the given sets:
- \(A = \{\textrm{ lines in the plane}\}\text{,}\) and \(R\) defined by \(x R y\) if and only if \(x\) is parallel to \(y\text{.}\) Assume every line is parallel to itself.
- \(A = \mathbb{R}\) and \(R\) defined by \(x R y\) if and only if \(\lvert x -y \rvert \leq 7\text{.}\)
5.
Consider the relation on \(\{1, 2, 3, 4, 5, 6\}\) defined by \(R = \{(i,j):\enspace \lvert i - j\rvert = 2\}\text{.}\)
- Is \(R\) reflexive?
- Is \(R\) symmetric?
- Is \(R\) transitive?
- Draw a graph of \(R\text{.}\)
Answer.
- No, since \(\mid 1-1\mid =0\neq 2\text{,}\) for example
- Yes, because \(\mid i-j\mid =\)\(\mid j-i\mid \text{.}\)
- No, since \(\mid 2-4\mid =2\) and \(\mid 4-6\mid =2\text{,}\) but \(\mid 2-6\mid =4\neq 2\text{,}\) for example.
6.
For the set of cities on a map, consider the relation \(x R y\) if and only if city \(x\) is connected by a road to city \(y\text{.}\) A city is considered to be connected to itself, and two cities are connected even though there are cities on the road between them. Is this an equivalence relation or a partial ordering? Explain.
7. Equivalence Classes.
Let \(A = \{0, 1, 2, 3\}\) and let
\begin{equation*}
R = \{(0, 0), (1, 1), (2, 2), (3, 3), (1, 2),(2, 1), (3, 2), (2, 3), (3, 1), (1, 3)\}
\end{equation*}
- Verify that \(R\) is an equivalence relation on \(A\text{.}\)
- Let \(a \in A\) and define \(c(a) = \{b \in A \mid a R b\}\text{.}\) \(c(a)\) is called the equivalence class of \(a\) under \(R\). Find \(c(a)\) for each element \(a \in A\text{.}\)
- Show that \(\{c(a) \mid a \in A\}\) forms a partition of \(A\) for this set \(A\text{.}\)
- Let \(R\) be an equivalence relation on an arbitrary set \(A\text{.}\) Prove that the set of all equivalence classes under \(R\) constitutes a partition of \(A\text{.}\)
Answer.
- It must be shown that \(R\) is reflexive, symmetric, and transitive.
- \(\displaystyle c(0)=\{0\}, c(1)=\{1,2,3\}=c(2)=c(3)\)
- \(c(0)\cup c(1)=A\) and \(c(0)\cap c(1)=\emptyset\)
-
Let \(A\) be any set and let \(R\) be an equivalence relation on \(A\text{.}\) Let \(a\) be any element of \(A\text{.}\) \(a\in c(a)\) since \(R\) is reflexive, so each element of \(A\) is in some equivalence class. Therefore, the union of all equivalence classes equals \(A\text{.}\) Next we show that any two equivalence classes are either identical or disjoint and we are done. Let \(c(a)\) and \(c(b)\) be two equivalence classes, and assume that \(c(a)\cap c(b)\neq \emptyset\text{.}\) We want to show that \(c(a)=c(b)\text{.}\) To show that \(c(a)\subseteq c(b)\text{,}\) let \(x\in c(a)\text{.}\) \(x\in c(a) \Rightarrow a R x \text{.}\) Also, there exists an element, \(y\text{,}\) of \(A\) that is in the intersection of \(c(a)\) and \(c(b)\) by our assumption. Therefore,\begin{equation*} \begin{split} a r y \land b R y &\Rightarrow a R y \land y R b \quad R\textrm{ is symmetric}\\ &\Rightarrow a R b \quad \textrm{ transitivity of }R \\ \end{split} \end{equation*}Next,\begin{equation*} \begin{split} a R x \land a R b &\Rightarrow x R a \land a R b\\ &\Rightarrow x R b\\ &\Rightarrow b R x\\ & \Rightarrow x \in c(b)\\ \end{split} \end{equation*}Similarly, \(c(b)\subseteq c(a)\text{.}\) \(\square\)
8.
Define \(R\) on the power set of \(S = \{1, 2, 3\}\) by \(A \, R \, B \Leftrightarrow \lvert A \rvert = \lvert B \rvert \text{,}\) where \(A,B \subseteq S\text{.}\) Prove that \(R\) is an equivalence relation. What are the equivalence classes under \(R\text{?}\)
9.
Consider the following relations on \(\mathbb{Z}_8= \{0, 1, . . . , 7\}\text{.}\) Which are equivalence relations? For the equivalence relations, list the equivalence classes.
- \(a R b\) iff the English spellings of \(a\) and \(b\) begin with the same letter.
- \(a S b\) iff \(a - b\) is a positive integer.
- \(a T b\) iff \(a-b\) is an even integer.
Answer.
- Equivalence Relation, \(c(0)=\{0\},c(1)=\{1\},c(2)=\{2,3\} =c(3),c(4)=\{4,5\}=c(5)\text{,}\) and \(c(6)=\{6,7\}=c(7)\)
- Not an Equivalence Relation.
- Equivalence Relation, \(c(0)=\{0,2,4,6\}=c(2)=c(4)=c(6)\) and \(c(1)=\{1,3,5,7\}=c(3)=c(5)=c(7)\)
10.
Building on Exercise 10.3.4.7:
- Prove that congruence modulo \(m\) is transitive.
- What are the equivalence classes under congruence modulo 2?
- What are the equivalence classes under congruence modulo 10?
11.
In this exercise, we prove that implication is a partial ordering. Let \(A\) be any set of propositions.
- Verify that \(q \to q\) is a tautology, thereby showing that \(\Rightarrow\) is a reflexive relation on \(A\text{.}\)
- Prove that \(\Rightarrow\) is antisymmetric on \(A\text{.}\) Note: we do not use = when speaking of propositions, but rather equivalence, \(\Leftrightarrow\text{.}\)
- Prove that \(\Rightarrow\) is transitive on \(A\text{.}\)
- Given that \(q_i\) is the proposition \(n < i\) on \(\mathbb{N}\text{,}\) draw the Hasse diagram for the relation \(\Rightarrow\) on \(\{q_1, q_2, q_3,\ldots \}\text{.}\)
Answer.
- These proofs follow from the biconditional equivalence in Table 4.4.4.
- Apply the chain rule.
Figure 10.3.21.
12.
Let \(S = \{1,2,3,4,5,6,7\}\) be a poset \((S, \leq )\) with the Hasse diagram shown below. Another relation \(R \subseteq S\times S\) is defined as follows: \((x, y) \in R\) if and only if there exists \(z \in S\) such that \(z < x\) and \(z < y\) in the poset \((S, \leq )\text{.}\)
- Prove that \(R\) is reflexive.
- Prove that \(R\) is symmetric.
- A compatible with respect to relation \(R\) is any subset \(Q\) of set \(S\) such that \(x \in Q \textrm{ and } y \in Q \Rightarrow (x, y) \in R\text{.}\) A compatible \(g\) is a maximal compatible if \(Q\) is not a proper subset of another compatible. Give all maximal compatibles with respect to relation \(R\) defined above.
- Discuss a characterization of the set of maximal compatibles for relation \(R\) when \((S, \leq )\) is a general finite poset. What conditions, if any, on a general finite poset \((S, \leq )\) will make \(R\) an equivalence relation?
