Section 13.3 Connectivity
¶This section is devoted to a question that, when posed in relation to the graphs that we have examined, seems trivial. That question is: Given two vertices, \(s\) and \(t\text{,}\) of a graph, is there a path from \(s\) to \(t\text{?}\) If \(s = t\text{,}\) this question is interpreted as asking whether there is a circuit of positive length starting at \(s\text{.}\) Of course, for the graphs we have seen up to now, this question can be answered after a brief examination.
Subsection 13.3.1 Preliminaries
¶There are two situations under which a question of this kind is nontrivial. One is where the graph is very large and an “examination” of the graph could take a considerable amount of time. Anyone who has tried to solve a maze may have run into a similar problem. The second interesting situation is when we want to pose the question to a machine. If only the information on the edges between the vertices is part of the data structure for the graph, how can you put that information together to determine whether two vertices can be connected by a path?
Note 13.3.1. Connectivity Terminology.
Let \(v\) and \(w\) be vertices of a directed graph. Vertex \(v\) is connected to vertex \(w\) if there is a path from \(v\) to \(w\text{.}\) Two vertices are strongly connected if they are connected in both directions to one another. A graph is connected if, for each pair of distinct vertices, \(v\) and \(w\text{,}\) \(v\) is connected to \(w\) or \(w\) is connected to \(v\text{.}\) A graph is strongly connected if every pair of its vertices is strongly connected. For an undirected graph, in which edges can be used in either direction, the notions of strongly connected and connected are the same.
Theorem 13.3.2. Maximal Path Theorem.
If a graph has \(n\) vertices and vertex \(u\) is connected to vertex \(w\text{,}\) then there exists a path from \(u\) to \(w\) of length no more than \(n\text{.}\)
Proof.
(Indirect): Suppose \(u\) is connected to \(w\text{,}\) but the shortest path from \(u\) to \(w\) has length \(m\text{,}\) where \(m>n\text{.}\) A vertex list for a path of length \(m\) will have \(m + 1\) vertices. This path can be represented as \(\left(v_0,v_1,\ldots, v_m\right)\text{,}\) where \(v_0=u\) and \(v_m= w\text{.}\) Note that since there are only \(n\) vertices in the graph and \(m\) vertices are listed in the path after \(v_0\text{,}\) we can apply the pigeonhole principle and be assured that there must be some duplication in the last \(m\) vertices of the vertex list, which represents a circuit in the path. This means that our path of minimum length can be reduced, which is a contradiction.
Subsection 13.3.2 Adjacency Matrix Method
¶Algorithm 13.3.3. Adjacency Matrix Method.
Suppose that the information about edges in a graph is stored in an adjacency matrix, \(G\text{.}\) The relation, \(r\text{,}\) that \(G\) defines is \(v r w\) if there is an edge connecting \(v\) to \(w\text{.}\) Recall that the composition of \(r\) with itself, \(r^2\text{,}\) is defined by \(v r^2 w\) if there exists a vertex \(y\) such that \(v r y\) and \(y r w\text{;}\) that is, \(v\) is connected to \(w\) by a path of length 2. We could prove by induction that the relation \(r^k\text{,}\) \(k\geq 1\text{,}\) is defined by \(v r^k w\) if and only if there is a path of length \(k\) from \(v\) to \(w\text{.}\) Since the transitive closure, \(r^+\text{,}\) is the union of \(r\text{,}\) \(r^2\) \(,r^3,\ldots\text{,}\) we can answer our connectivity question by determining the transitive closure of \(r\text{,}\) which can be done most easily by keeping our relation in matrix form. Theorem 13.3.2 is significant in our calculations because it tells us that we need only go as far as \(G^n\) to determine the matrix of the transitive closure.
The main advantage of the adjacency matrix method is that the transitive closure matrix can answer all questions about the existence of paths between any vertices. If \(G^+\) is the matrix of the transitive closure, \(v_i\) is connected to \(v_j\) if and only if \(\left(G^+\right)_{i j }=1\text{.}\) A directed graph is connected if \(\left(G^+\right)_{i j }=1\) or \(\left(G^+\right)_{j i}=1\) for each \(i\neq j\text{.}\) A directed graph is strongly connected if its transitive closure matrix has no zeros.
A disadvantage of the adjacency matrix method is that the transitive closure matrix tells us whether a path exists, but not what the path is. The next algorithm will solve this problem.
Subsection 13.3.3 Breadth-First Search
¶We will describe the Breadth-First Search Algorithm first with an example.
The football team at Mediocre State University (MSU) has had a bad year, 2 wins and 9 losses. Thirty days after the end of the football season, the university trustees are meeting to decide whether to rehire the head coach; things look bad for him. However, on the day of the meeting, the coach issues the following press release with results from the past year:
The Mediocre State University football team compared favorably with national champion Enormous State University this season.
Mediocre State defeated Local A and M.
Local A and M defeated City College.
City College defeated Corn State U.
... (25 results later)
Tough Tech defeated Enormous State University (ESU).
...and ESU went on to win the national championship!
The trustees were so impressed that they rehired the coach with a raise! How did the coach come up with such a list?
In reality, such lists exist occasionally and have appeared in newspapers from time to time. Of course they really don't prove anything since each team that defeated MSU in our example above can produce a similar, shorter chain of results. Since college football records are readily available, the coach could have found this list by trial and error. All that he needed to start with was that his team won at least one game. Since ESU lost one game, there was some hope of producing the chain.
The problem of finding this list is equivalent to finding a path in the tournament graph for last year's football season that initiates at MSU and ends at ESU. Such a graph is far from complete and is likely to be represented using edge lists. To make the coach's problem interesting, let's imagine that only the winner of any game remembers the result of the game. The coach's problem has now taken on the flavor of a maze. To reach ESU, he must communicate with the various teams along the path. One way that the coach could have discovered his list in time is by sending the following messages to the coaches of the two teams that MSU defeated during the season:
Note 13.3.5.
When this example was first written, we commented that ties should be ignored. Most recent NCAA rules call for a tiebreaker in college football and so ties are no longer an issue. Email was also not common and we described the process in terms of letter, not email messages. Another change is that the coach could also have asked the MSU math department to use Mathematica or Sage to find the path!
Dear Football Coach:
Please follow these directions exactly.
If you are the coach at ESU, contact the coach at MSU now and tell him who sent you this message.
-
If you are not the coach at ESU and this is the first message of this type that you have received, then:
Remember from whom you received this message.
Forward a copy of this message, signed by you, to each of the coaches whose teams you defeated during the past year.
Ignore this message if you have received one like it already.
\(\quad \quad \quad \quad \quad \)Signed,
\(\quad \quad \quad \quad \quad \)Coach of MSU
From the conditions of this message, it should be clear that if everyone cooperates and if coaches participate within a day of receiving the message:
If a path of length \(n\) exists from MSU to ESU, then the coach will know about it in \(n\) days.
By making a series of phone calls, the coach can construct a path that he wants by first calling the coach who defeated ESU (the person who sent ESU's coach that message). This coach will know who sent him a letter, and so on. Therefore, the vertex list of the desired path is constructed in reverse order.
If a total of \(M\) football games were played, no more than \(M\) messages will be sent out.
If a day passes without any message being sent out, no path from MSU to ESU exists.
This method could be extended to construct a list of all teams that a given team can be connected to. Simply imagine a series of letters like the one above sent by each football coach and targeted at every other coach.
The general problem of finding a path between two vertices in a graph, if one exists, can be solved exactly as we solved the problem above. The following algorithm, commonly called a breadth-first search, uses a stack.
Algorithm 13.3.8. Breadth-first Search.
A broadcasting algorithm for finding a path between vertex \(i\) and vertex \(j\) of a graph having \(n\) vertices. Each item \(V_k\) of a list \(V=\left\{V_1, V_2, \ldots , V_n\right\}\text{,}\) consists of a Boolean field \(V_k.\text{found}\) and an integer field \(V_k.\text{from}\text{.}\) The sets \(D_1\text{,}\) \(D_2, \dots\text{,}\) called depth sets, have the property that if \(k \in D_r\text{,}\) then the shortest path from vertex \(i\) to vertex \(k\) is of length \(r\text{.}\) In Step 5, a stack is used to put the vertex list for the path from the vertex \(i\) to vertex \(j\) in the proper order. That stack is the output of the algorithm.
Set the value \(V_k.\text{found}\) equal to False, \(k = 1, 2, \dots , n\)
\(r = 0\)
\(D_0= \{i\}\)
-
while \((\neg V_j.\text{found}\)) and \(\left(D_r\right.\neq \emptyset )\)
\(D_{r+1}=\emptyset\)
-
for each k in \(D_r\text{:}\)
\(\quad\)for each edge (k,t):
\(\quad \quad \)If \(V_t.\text{found}\) == False:
\(\quad \quad \quad \)\(V_t.\text{found}=\text{True}\)
\(\quad \quad \quad \)\(V_t.\text{from} = k\)
\(\quad \quad \quad \)\(D_{r+1}=D_{r+1}\cup \{t\}\)
\(r = r + 1\)
-
if \(V_j.\text{found}\text{:}\)
\(S = Empty Stack\)
\(k=j\)
-
while \(V_k.\text{from} \neq i\text{:}\)
\(\quad\)Push \(k\) onto \(S\)
\(\quad\)\(k = V_k.\text{from}\)
Push \(k\) onto \(S\)
Push \(i\) onto \(S\)
This algorithm will produce one path from vertex \(i\) to vertex \(j\text{,}\) if one exists, and that path will be as short as possible. If more than one path of this length exists, then the one that is produced depends on the order in which the edges are examined and the order in which the elements of \(D_r\) are examined in Step 4.
The condition \(D_{r }\neq \emptyset\) is analogous to the condition that no mail is sent in a given stage of the process, in which case MSU cannot be connected to ESU.
This algorithm can be easily revised to find paths to all vertices that can be reached from vertex \(i\text{.}\) Step 5 would be put off until a specific path to a vertex is needed since the information in \(V\) contains an efficient list of all paths. The algorithm can also be extended further to find paths between any two vertices.
Example 13.3.10. A simple example.
Consider the graph below. The existence of a path from vertex 2 to vertex 3 is not difficult to determine by examination. After a few seconds, you should be able to find two paths of length four. Algorithm 13.3.8 will produce one of them.
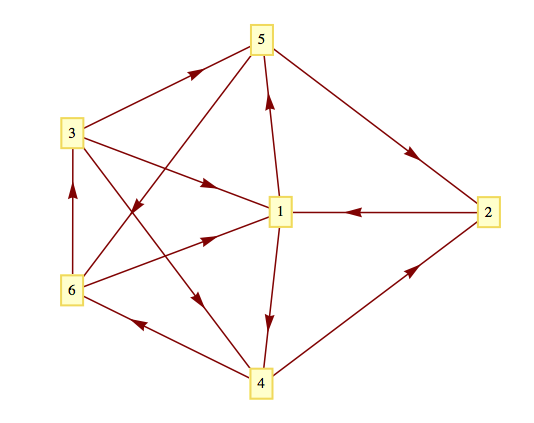
Suppose that the edges from each vertex are sorted in ascending order by terminal vertex. For example, the edges from vertex 3 would be in the order \((3, 1), (3, 4), (3, 5)\text{.}\) In addition, assume that in the body of Step 4 of the algorithm, the elements of \(D_r\) are used in ascending order. Then at the end of Step 4, the value of \(V\) will be
Therefore, the path \((2, 1, 4, 6, 3)\) is produced by the algorithm. Note that if we wanted a path from 2 to 5, the information in \(V\) produces the path (2, 1, 5) since \(V_k.\text{from} = 1\) and \(V_1.\text{from} = 2\text{.}\) A shortest circuit that initiates at vertex 2 is also available by noting that \(V_2.\text{from}=4\text{,}\) \(V_4\text{.from = 1}\text{,}\) and \(V_1.\text{from} = 2\text{;}\) thus the circuit \((2, 1, 4, 2)\) is the output of the algorithm.
Subsection 13.3.4 SageMath Note - Graph Searching
¶The following sequence of Sage cells illustrates how searching can be done in graphs.
Generate a random undirected graph with 18 vertices. For each pair of vertices, an edge is included between them with probability 0.2. Since there are \(\binom{18}{2}=153\) potential edges, we expect that there will be approximately \(0.2 \cdot 153 \approx 31\) edges. The random number generation is seeded first so that the result will always be the same in spite of the random graph function. Changing or removing that first line will let you experiment with different graphs.
Count the number of edges. In this case the number is a bit less than expected.
Find a shortest path from vertex 0 to vertex 8.
Generate a list of vertices that would be reached in a breadth-first search. The expression Gr.breadth_first_search(0) creates an iterator that is convenient for programming. Wrapping list( ) around the expression shows the order in which the vertices are visited with the depth set indicated in the second coordinates.
Generate a list of vertices that would be reached in a depth-first search. In this type of search you travel in one direction away from the starting point until no further new vertices can be reached. We will discuss this search later.
Exercises 13.3.5 Exercises
¶1.
Apply Algorithm 13.3.8 to find a path from 5 to 1 in Figure 13.3.11. What would be the final value of \(V\text{?}\) Assume that the terminal vertices in edge lists and elements of the depth sets are put into ascending order, as we assumed in Example 13.3.10.
\(\begin{array}{ccccccc} k & 1 & 2 & 3 & 4 & 5 & 6 \\ V[k].\text{found} & T & T & T & F & F & T \\ V[k].\text{from} & 2 & 5 & 6 & * & * & 5 \\ \text{Depth} \text{Set} & 2 & 1 & 2 & * & * & 1 \\ \end{array}\) \(\text{(*} = \text{undefined})\)
2.
Apply Algorithm 13.3.8 to find a path from \(d\) to \(c\) in the road graph in Example 13.1.9 using the edge list in that example. Assume that the elements of the depth sets are put into ascending order.
3.
In a simple undirected graph with no self-loops, what is the maximum number of edges you can have, keeping the graph unconnected? What is the minimum number of edges that will assure that the graph is connected?
If the number of vertices is \(n\text{,}\) there can be \(\frac{(n-1)(n-2)}{2}\) vertices with one vertex not connected to any of the others. One more edge and connectivity is assured.
4.
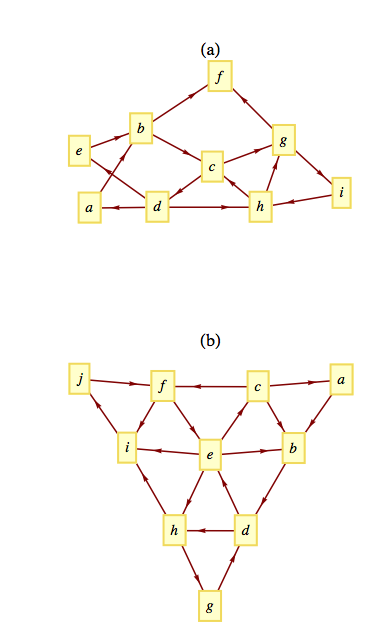
Use a broadcasting algorithm to determine the shortest path from vertex \(a\) to vertex \(i\) in the graphs shown in the Figure 13.3.12 below. List the depth sets and the stack that is created.
5.
Prove (by induction on \(k\)) that if the relation \(r\) on vertices of a graph is defined by \(v r w\) if there is an edge connecting \(v\) to \(w\text{,}\) then \(r^k\text{,}\) \(k \geq 1\text{,}\) is defined by \(v r^kw\) if there is a path of length \(k\) from \(v\) to \(w\text{.}\)
Basis: \((k=1)\) Is the relation \(r^1\text{,}\) defined by \(v r^1 w\) if there is a path of length 1 from \(v \text{ to } w\text{?}\) Yes, since \(v r w\) if and only if an edge, which is a path of length \(1\text{,}\) connects \(v\) to \(w\text{.}\)
Induction: Assume that \(v r^k w\) if and only if there is a path of length \(k\) from \(v\) to \(w\text{.}\) We must show that \(v r^{k+1} w\) if and only if there is a path of length \(k+1\) from \(v\) to \(w\text{.}\)
By the induction hypothesis, there is a path of length \(k\) from \(v \textrm{ to } y\text{.}\) And by the basis, there is a path of length one from \(y\) to \(w\text{.}\) If we combine these two paths, we obtain a path of length \(k+1\) from \(v\) to \(w\text{.}\) Of course, if we start with a path of length \(k+1\) from \(v\) to \(w\text{,}\) we have a path of length \(k\) from \(v\) to some vertex \(y\) and a path of length 1 from \(y\) to \(w\text{.}\) Therefore, \(v r^k y \textrm{ and } y r w \Rightarrow v r^{k+1} w\text{.}\)