Discrete Mathematics for Computer Science

Section 12.7 Logic Gates and Circuits

Early computers relied on many switches to perform the logical operations needed for computation. This was true as late as the 1970's when early personal computers such as the Altair ( Figure 12.7.1) started to appear. Pioneering computer scientists such as Claude Shannon realized that the operation of these computers could be simplified by making use of an isomorphism between computer circuits and boolean algebra. The term Switching Theory was used at the time. Logical gates realized through increasingly smaller and smaller integrated circuits still perform the same functions as in early computers, but using purely electronic means. In this section, we give examples of some switching circuits. Soon afterward, we will transition to the more modern form of circuits that are studied in Logic Design, where gates replace switches. Our main goal is to give you an overview of how boolean functions correspond to actual computer circuits. We will introduce the common system notation used in logic design and show how it corresponds with the mathematical notation of Boolean algebras. Any computer scientist should be familiar with both systems.

The simplest switching device is the on-off switch. If the switch is closed/ON, electrical current will pass through it; if it is open/OFF, current will not pass through it. If we designate ON by 1, and OFF by 0, we can describe electrical circuits containing switches by Boolean expressions with the variables representing the variable states of switches or the variable bits passing through gates.

The electronics involved in these switches take into account whether we are negating a switch or not. For electromagnetic switches, a magnet is used to control whether the switch is open or closed. The magnets themselves may be controlled by simple ON/OFF switches. There are two types of electromagnetic switches. One is normally open (OFF) when the magnet is not activated, but activating the magnet will close the circuit and the switch is then ON. A separate type of switch corresponds with a negated switch. For that type, the switch is closed (ON) when the magnet is not activated, and when the magnet is activated, the switch opens (turns OFF). We won't be overly concerned with the details of these switches or the electronics corresponding to logical gates. We will simply assume they are available to plug into a circuit. For simplicity, we use the complement symbol on a varible that labels a switch to indicate that it is a switch of the second type, as in Figure 12.7.3.

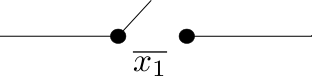
The standard notation used for Boolean algebra operations in switching theory and logic design is \(+\) for join, instead of \(\lor \text{;}\) and \(\cdot \) for meet, instead of \(\land \text{.}\) Complementation is the same in both notational systems, denoted with an overline.

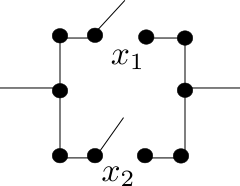
The expression \(x_1 \cdot x_2\) represents the situation in which a series of two switches appears in sequence as in Figure 12.7.4. In order for current to flow through the circuit, both switches must be ON; that is, \(x_1\) AND \(x_2\) must both have the value 1. Similarly, a pair of parallel switches, as in Figure 12.7.5, is described algebraically by \(x_1 + x_2\text{.}\) Here, current flows through this part of the circuit as long as at least one of the switches, \(x_1\) OR \(x_2\text{,}\) is ON.

All laws and concepts developed previously for Boolean algebras hold. The only change is purely notational. We make the change in this section solely to introduce the reader to another frequently used system of notation.

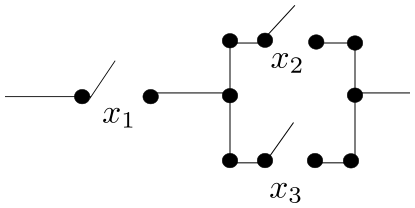
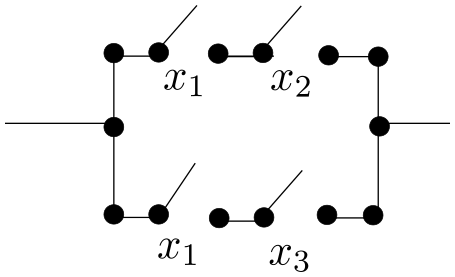
Many of the laws of Boolean algebra can be visualized thought switching theory. For example, the distributive law of meet over join is expressed as

The switching circuit analogue of the above statement is that the circuits in the two images below are equivalent. In circuit (b), the presence of two \(x_1\)'s might represent two electromagnetic switches controlled by the same magnet.

The circuits in a computer are now composed of large quantities of gates, which serve the same purpose as switches, but can be miniaturized to a great degree. For example, the OR gate, usually drawn as in Figure 12.7.8 implements the logical OR function. This happens electronically, but is equivalent to Figure 12.7.5. The AND gate, which is equivalent to two sequential switches is shown in Figure 12.7.8.

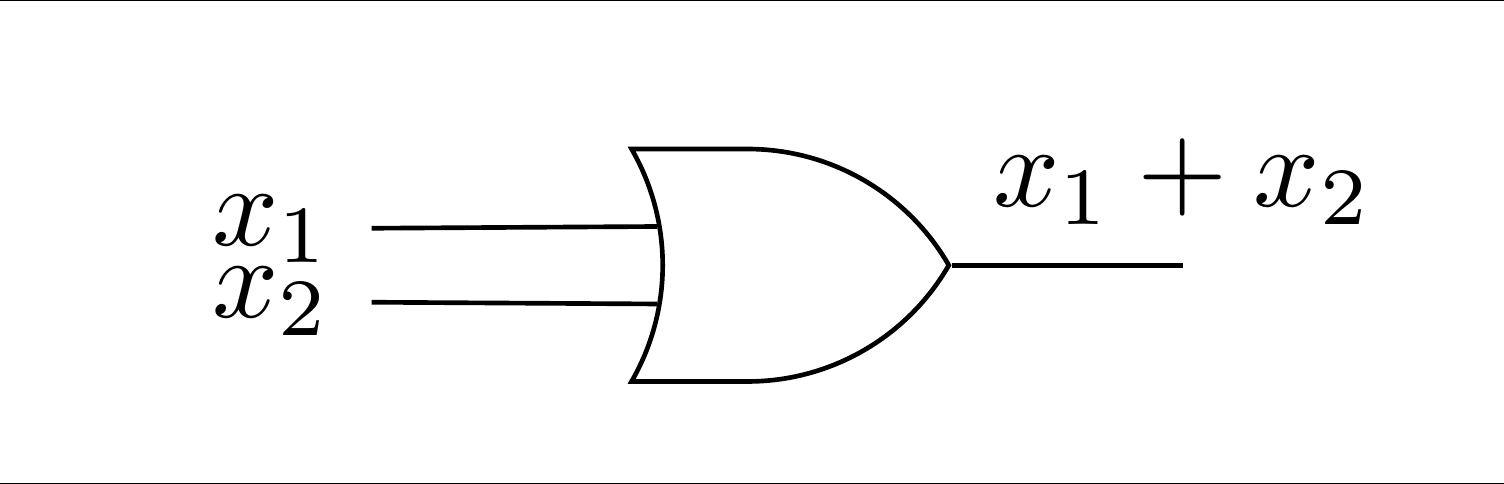
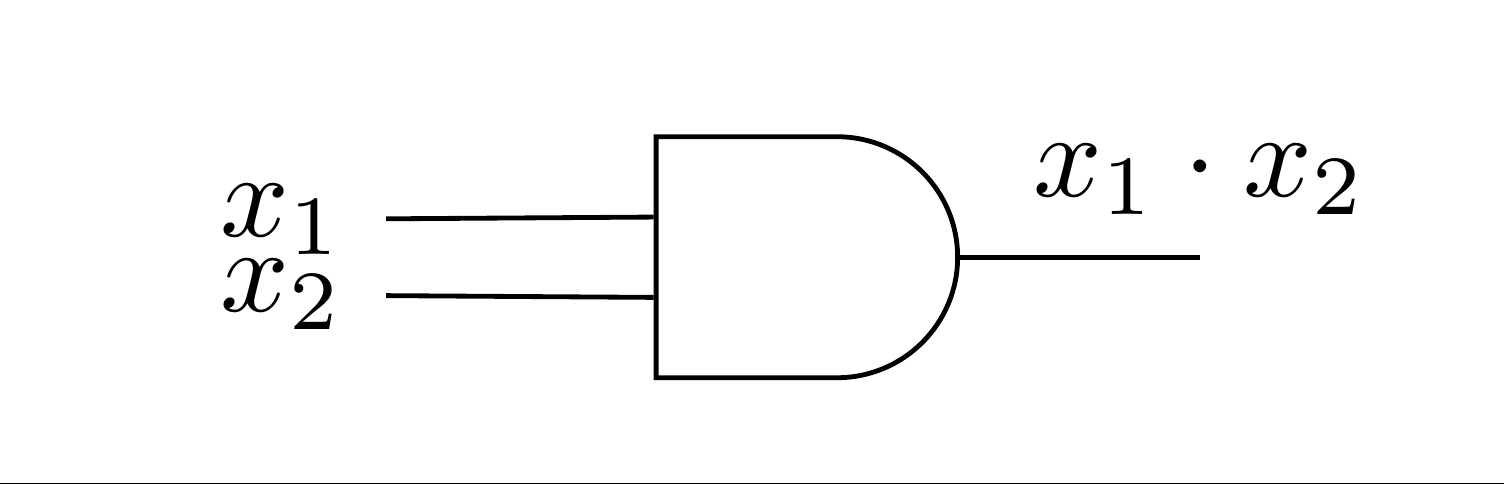
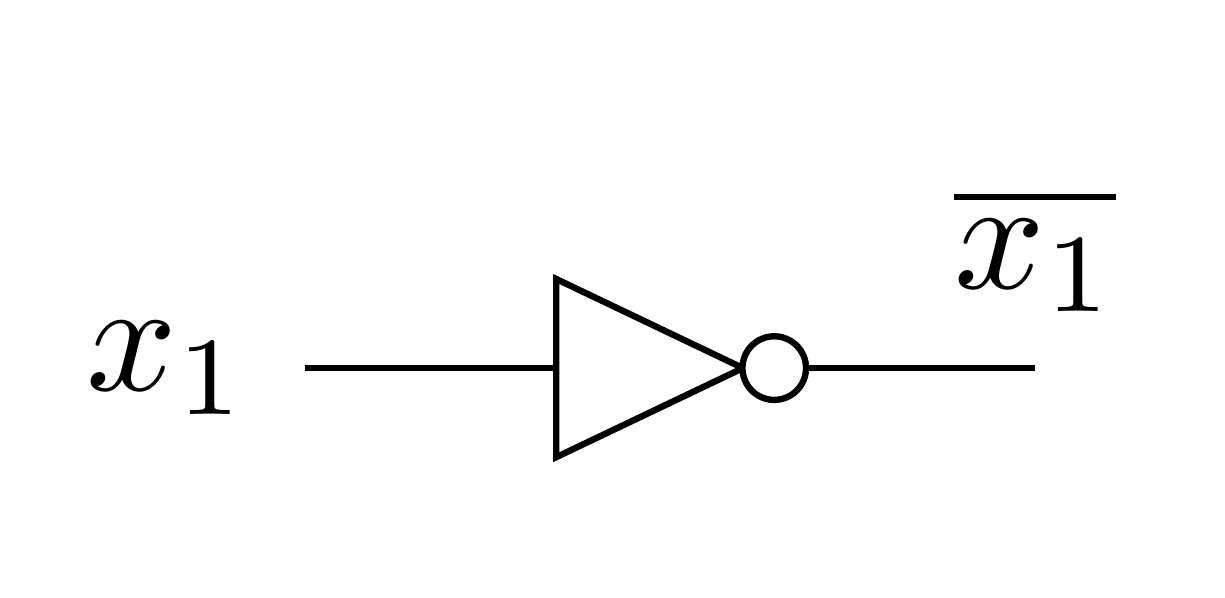
The complementation process is represented in a gate diagram by an inverter, as pictured in Figure 12.7.10.

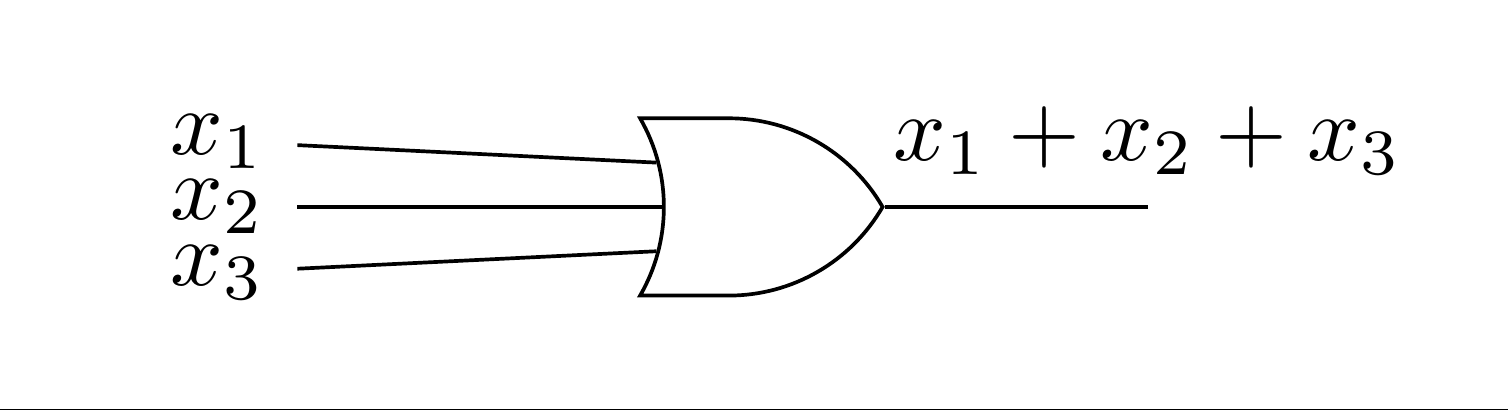
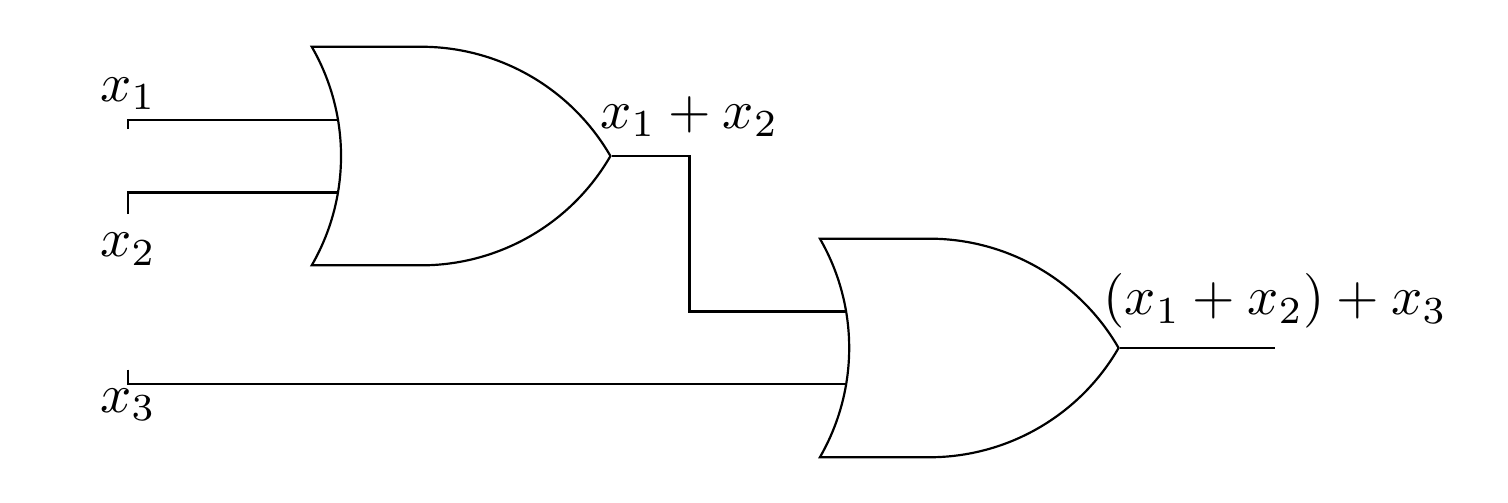
When drawing more complex circuits, multiple AND's or OR's are sometimes depicted using a more general gate drawing. For example if we want to depict an OR gate with three inputs that is ON as long as at least one input is ON, we would draw it as in Figure 12.7.11, although this would really be two binary gates, as in Figure 12.7.12. Both diagrams are realizing the boolean expression \(x_1 + x_2 + x_3\text{.}\) Strictly speaking, the gates in Figure 12.7.12 represent \((x_1 + x_2 )+ x_3\text{,}\) but the associative law for join tells us that the grouping doesn't matter.

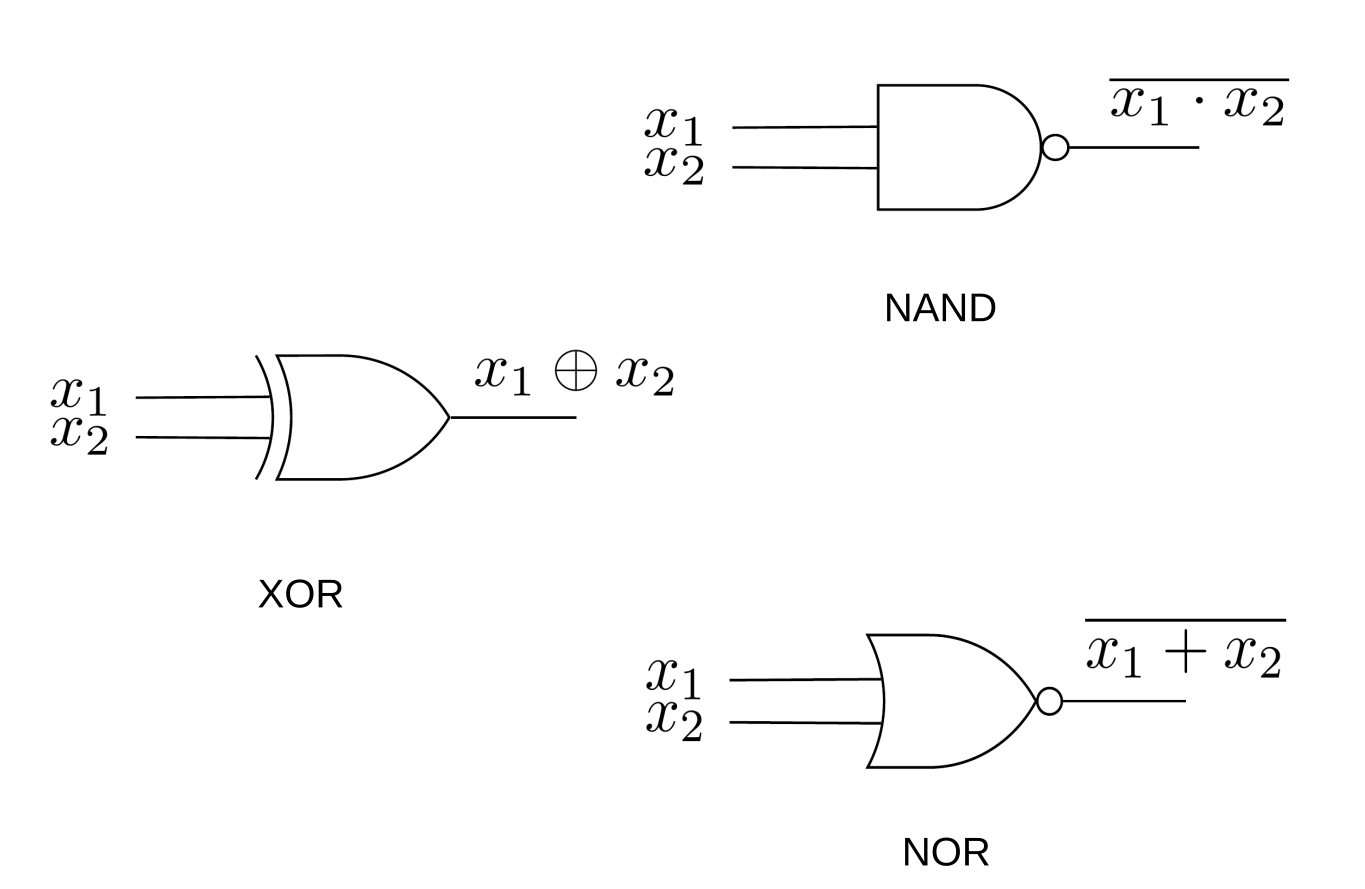
In Figure 12.7.13, we show a few other commonly used gates, XOR, NAND, and NOR, which correspond to the boolean exressions \(x_1 \oplus x_2\text{,}\) \(\overline{x_1 \cdot x_2}\text{,}\) and \(\overline{x_1 + x_2}\text{,}\) respectively.