Section 10.2 Graphs of Relations on a Set
¶In this section we introduce directed graphs as a way to visualize relations on a set.
Subsection 10.2.1 Digraphs
Let \(A = \{0, 1,2,3\}\text{,}\) and let
In representing this relation as a graph, elements of \(A\) are called the vertices of the graph. They are typically represented by labeled points or small circles. We connect vertex \(a\) to vertex \(b\) with an arrow, called an edge, going from vertex \(a\) to vertex \(b\) if and only if \(a R b\text{.}\) This type of graph of a relation \(R\) is called a directed graph or digraph. Figure 10.2.1 is a digraph for \(R\text{.}\) Notice that since 0 is related to itself, we draw a “self-loop” at 0.
The actual location of the vertices in a digraph is immaterial. The actual location of vertices we choose is called an embedding of a graph. The main idea is to place the vertices in such a way that the graph is easy to read. After drawing a rough-draft graph of a relation, we may decide to relocate the vertices so that the final result will be neater. Figure 10.2.1 could also be presented as in Figure 10.2.2.
A vertex of a graph is also called a node, point, or a junction. An edge of a graph is also referred to as an arc, a line, or a branch. Do not be concerned if two graphs of a given relation look different as long as the connections between vertices are the same in two graphs.
Example 10.2.3. Another directed graph.
Consider the relation \(R\) whose digraph is Figure 10.2.4. What information does this give us? The graph tells us that \(R\) is a relation on \(A = \{1, 2, 3\}\) and that \(R = \{(1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 3)\}\text{.}\)
We will be building on the next example in the following section.
Example 10.2.5. Ordering subsets of a two element universe.
Let \(B = \{1,2\}\text{,}\) and let \(A = \mathcal{P}(B) = \{\emptyset, \{1\}, \{2\}, \{1,2\}\}\text{.}\) Then \(\subseteq\) is a relation on \(A\) whose digraph is Figure 10.2.6.
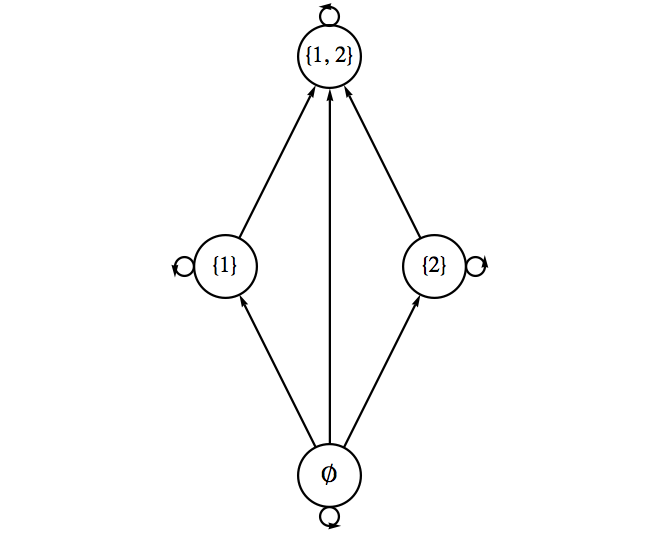
We will see in the next section that since \(\subseteq\) has certain structural properties that describe “partial orderings.” We will be able to draw a much simpler type graph than this one, but for now the graph above serves our purposes.
Exercises 10.2.2 Exercises
¶1.
Let \(A = \{1, 2, 3, 4\}\text{,}\) and let \(R\) be the relation \(\leq\) on \(A\text{.}\) Draw a digraph for \(R\text{.}\)
2.
Let \(B = \{1,2, 3, 4, 6, 8, 12, 24\}\text{,}\) and let \(R\) be the relation “divides” on \(B\text{.}\) Draw a digraph for \(R\text{.}\)
3.
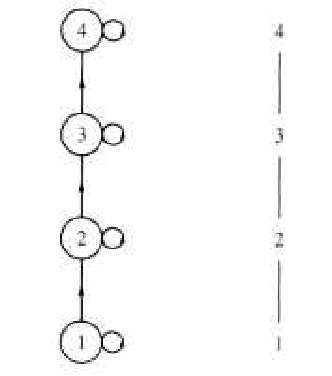
Let \(A=\{1,2,3,4,5\}\text{.}\) Define \(T\) on \(A\) by \(a T b\) if and only if \(b - a\) is even. Draw a digraph for \(T\text{.}\)
See Figure 10.2.8
4.
- Let \(A\) be the set of strings of 0's and 1's of length 3 or less. Define the relation of \(D\) on \(A\) by \(x D y\) if \(x\) is contained within \(y\text{.}\) For example, \(01 D 101\text{.}\) Draw a digraph for this relation.
- Do the same for the relation \(P\) defined by \(x P y\) if \(x\) is a prefix of \(y\text{.}\) For example, \(10 P 101\text{,}\) but \(01 P 101\) is false.
5.
Recall the relation in Exercise 5 of Section 10.1, \(\rho\) defined on the power set, \(\mathcal{P}(S)\text{,}\) of a set \(S\text{.}\) The definition was \((A,B) \in \rho\) iff \(A\cap B = \emptyset\text{.}\) Draw the digraph for \(\rho\) where \(S = \{a, b\}\text{.}\)
6.
Let \(C= \{1,2, 3, 4, 6, 8, 12, 24\}\) and define \(T\) on \(C\) by \(a T b\) if and only if \(a\) and \(b\) share a common divisor greater than 1. Draw a digraph for \(T\text{.}\)